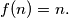Let  be an even positive integer. Let
be an even positive integer. Let 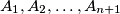 be sets having
be sets having  elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which
elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which  can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly
can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly 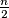 zeros?
zeros?
 be an even positive integer. Let
be an even positive integer. Let 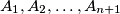 be sets having
be sets having  elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which
elements each such that any two of them have exactly one element in common while every element of their union belongs to at least two of the given sets. For which  can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly
can one assign to every element of the union one of the numbers 0 and 1 in such a manner that each of the sets has exactly 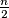 zeros?
zeros? Consider 2 concentric circle radii  and
and  (
(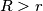 ) with centre
) with centre 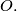 Fix
Fix  on the small circle and consider the variable chord
on the small circle and consider the variable chord 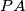 of the small circle. Points
of the small circle. Points  and
and  lie on the large circle;
lie on the large circle; 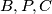 are collinear and
are collinear and  is perpendicular to
is perpendicular to 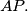
i.) For which values of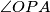 is the sum
is the sum 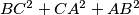 extremal?
extremal?
ii.) What are the possible positions of the midpoints of
of 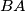 and
and  of
of  as
as 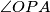 varies?
varies?
 and
and  (
(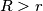 ) with centre
) with centre  Fix
Fix  on the small circle and consider the variable chord
on the small circle and consider the variable chord 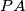 of the small circle. Points
of the small circle. Points  and
and  lie on the large circle;
lie on the large circle; 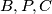 are collinear and
are collinear and  is perpendicular to
is perpendicular to 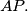
i.) For which values of
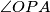 is the sum
is the sum 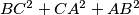 extremal?
extremal? ii.) What are the possible positions of the midpoints
 of
of 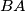 and
and  of
of  as
as 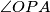 varies?
varies?  Školjka
Školjka 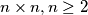 chessboard is numbered by the numbers
chessboard is numbered by the numbers 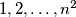 (and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least
(and every number occurs). Prove that there exist two neighbouring (with common edge) squares such that their numbers differ by at least 
 and
and  be two positive integers such that
be two positive integers such that 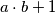 divides
divides 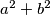 . Show that
. Show that 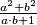 is a perfect square.
is a perfect square.  let
let  be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles
be the altitude drawn to the hypotenuse and let the straight line joining the incentres of the triangles 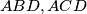 intersect the sides
intersect the sides 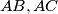 at the points
at the points 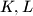 respectively. If
respectively. If  and
and 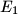 dnote the areas of triangles
dnote the areas of triangles 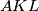 respectively, show that
respectively, show that 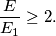
 defined on the positive integers (and taking positive integers values) is given by:
defined on the positive integers (and taking positive integers values) is given by: 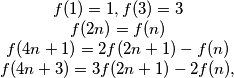
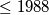 for which
for which