An international society has its members from six different countries. The list of members contain 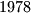 names, numbered
names, numbered 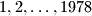 . Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
. Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
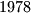 names, numbered
names, numbered 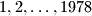 . Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
. Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country. We consider a fixed point  in the interior of a fixed sphere
in the interior of a fixed sphere We construct three segments
We construct three segments 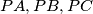 , perpendicular two by two
, perpendicular two by two with the vertexes
with the vertexes  on the sphere
on the sphere We consider the vertex
We consider the vertex  which is opposite to
which is opposite to  in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with 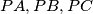 as edges
as edges Find the locus of the point
Find the locus of the point  when
when  take all the positions compatible with our problem.
take all the positions compatible with our problem.
 in the interior of a fixed sphere
in the interior of a fixed sphere We construct three segments
We construct three segments 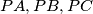 , perpendicular two by two
, perpendicular two by two with the vertexes
with the vertexes  on the sphere
on the sphere We consider the vertex
We consider the vertex  which is opposite to
which is opposite to  in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with 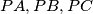 as edges
as edges Find the locus of the point
Find the locus of the point  when
when  take all the positions compatible with our problem.
take all the positions compatible with our problem.  Školjka
Školjka  and
and  be positive integers such that
be positive integers such that 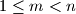 . In their decimal representations, the last three digits of
. In their decimal representations, the last three digits of 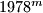 are equal, respectively, so the last three digits of
are equal, respectively, so the last three digits of 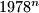 . Find
. Find 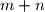 has its least value.
has its least value.  be an injective function from
be an injective function from 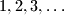 in itself. Prove that for any
in itself. Prove that for any 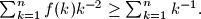
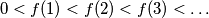 a sequence with all its terms positive
a sequence with all its terms positive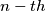 positive integer which doesn't belong to the sequence is
positive integer which doesn't belong to the sequence is 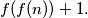 Find
Find 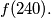
 we have
we have 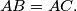 A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides
A circle which is internally tangent with the circumscribed circle of the triangle is also tangent to the sides 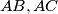 in the points
in the points 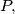 respectively
respectively 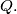 Prove that the midpoint of
Prove that the midpoint of  is the center of the inscribed circle of the triangle
is the center of the inscribed circle of the triangle 