Simulacije državnog natjecanja 2020.
Na ploči je napisano 2020 prirodnih brojeva. Svaku minutu, na ploču dopišemo novi red brojeva na sljedeći način. Ispod svakog broja  u prethodnom redu napišemo broj
u prethodnom redu napišemo broj 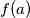 gdje
gdje 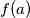 predstavlja broj pojavljivanja broja
predstavlja broj pojavljivanja broja  u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
u prethodnom redu. Dokažite da ćemo u nekom trenutku, jedan za drugim, napisati isti red brojeva.
Na kružnici je nasumično postavljeno  bijelih i
bijelih i  crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima
crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima 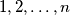 . Na isti način su i sve crne kuglice označene brojevima
. Na isti način su i sve crne kuglice označene brojevima 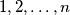 u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od
u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od  uzastopnih kuglica koje su označene brojevima
uzastopnih kuglica koje su označene brojevima 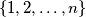 u nekom redoslijedu.
u nekom redoslijedu.
Neka je  prirodan broj veći od
prirodan broj veći od  . Na kružnici je
. Na kružnici je 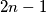 jednako udaljenih točaka od kojih je točno
jednako udaljenih točaka od kojih je točno  obojano crveno. Takvo bojanje zovemo
obojano crveno. Takvo bojanje zovemo 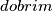 ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno
ako postoji barem jedan par crvenih točaka takvih da se unutar jednog luka koji taj par tvori nalazi točno  točaka. Odredi najmanji mogući
točaka. Odredi najmanji mogući  za koji je svako bojanje točaka na kružnici
za koji je svako bojanje točaka na kružnici 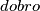 .
.
 Školjka
Školjka 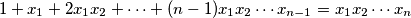 za različite prirodne brojeve
za različite prirodne brojeve 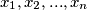 .
.  s ortocentrom
s ortocentrom  . Neka je
. Neka je  polovište stranice
polovište stranice  , a
, a  drugo sjecište pravca
drugo sjecište pravca 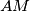 i opisane kružnice
i opisane kružnice  . Neka je
. Neka je  centralno simetrična slika točki
centralno simetrična slika točki 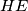 okomit na pravac
okomit na pravac  koji zadovoljavaju relaciju
koji zadovoljavaju relaciju 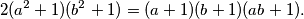
 i
i 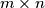 može popločati (bez preklapanja) figurama sastavljenih od jediničnih kvadrata kao na slici?
može popločati (bez preklapanja) figurama sastavljenih od jediničnih kvadrata kao na slici?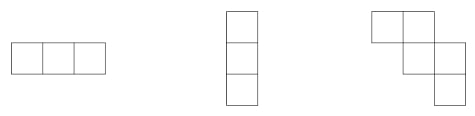
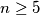 , brojevi
, brojevi 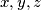 vrijedi
vrijedi 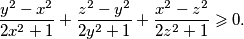
 i prirodne brojeve
i prirodne brojeve 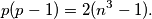
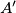 simetrična točki
simetrična točki  s obzirom na stranicu
s obzirom na stranicu  i
i  točke na stranicama
točke na stranicama  i
i  , redom, takve da je
, redom, takve da je 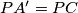 i
i 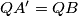 . Dokaži da okomica iz
. Dokaži da okomica iz  prolazi središtem opisane kružnice
prolazi središtem opisane kružnice 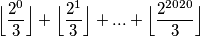
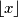 označava najveći cijeli broj manji od
označava najveći cijeli broj manji od  .
. 
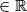 takvi da vrijedi
takvi da vrijedi 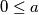 ,
, 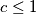 . Dokaži nejednakost:
. Dokaži nejednakost: 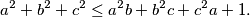
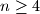 takav da za svaki skup
takav da za svaki skup  koji sadrži točno
koji sadrži točno  (različita) broja
(različita) broja  iz
iz 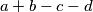 djeljiv s
djeljiv s  .
.  i u njemu točka
i u njemu točka  tako da vrijedi
tako da vrijedi 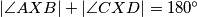 . Odredi vrijednost izraza:
. Odredi vrijednost izraza: 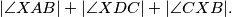
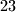 prijatelja igra nogomet. Prvo izaberu suca koji će momčadi podijeliti u
prijatelja igra nogomet. Prvo izaberu suca koji će momčadi podijeliti u  tima od
tima od  ljudi. Znamo da je težina svakog od njih prirodan broj i da je, bez obzira tko je sudac, uvijek moguće napraviti
ljudi. Znamo da je težina svakog od njih prirodan broj i da je, bez obzira tko je sudac, uvijek moguće napraviti 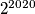 sa svojstvom da kada umnošku bilo koja
sa svojstvom da kada umnošku bilo koja  dobijemo potpuni kvadrat?
dobijemo potpuni kvadrat?  polinom sa realnim koeficijentima stupnja
polinom sa realnim koeficijentima stupnja 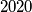 . Ako
. Ako 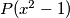 ima
ima 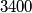 realnih nultočaka, a
realnih nultočaka, a 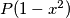 ima
ima 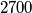 realnih nultočaka, dokaži da onda postoje dvije realne nultočke od
realnih nultočaka, dokaži da onda postoje dvije realne nultočke od 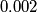 .
.  za koje vrijedi da je
za koje vrijedi da je 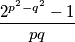 umnožak točno
umnožak točno  i
i 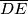 kružnice
kružnice  sijeku se u
sijeku se u  , a
, a 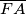 siječe
siječe  . Neka je
. Neka je 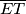 i
i  preslika
preslika 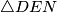 .
. 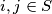 (može biti
(može biti 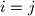 ) onda je i
) onda je i 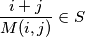 .
. 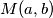 označava najveći zajednički dijelitelj brojeva
označava najveći zajednički dijelitelj brojeva