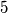
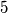
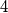
Given points in the plane, no three of them being collinear. Show that among these points, we can always find points forming a convex quadrilateral.
%V0
Given $5$ points in the plane, no three of them being collinear. Show that among these $5$ points, we can always find $4$ points forming a convex quadrilateral.
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
points in the plane, no three of them being collinear. Show that among these 
points forming a convex quadrilateral.