IMO Shortlist 1966 problem 5
Dodao/la:
arhiva2. travnja 2012. Prove the inequality
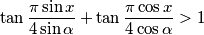
for any
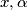
with
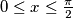
and

%V0
Prove the inequality
$$\tan \frac{\pi \sin x}{4\sin \alpha} + \tan \frac{\pi \cos x}{4\cos \alpha} >1$$
for any $x, \alpha$ with $0 \leq x \leq \frac{\pi }{2}$ and $\frac{\pi}{6} < \alpha < \frac{\pi}{3}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1966