IMO Shortlist 1966 problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a convex polygon in a plane,
be a convex polygon in a plane,  its perimeter and
its perimeter and  its area. Let
its area. Let 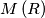 be the locus of all points in the space whose distance to
be the locus of all points in the space whose distance to  is
is 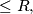 and
and 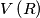 is the volume of the solid
is the volume of the solid 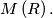
a.) Prove that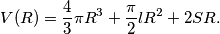
Hereby, we say that the distance of a point to a figure
to a figure  is
is 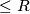 if there exists a point
if there exists a point  of the figure
of the figure  such that the distance
such that the distance  is
is 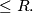 (This point
(This point  may lie on the boundary of the figure
may lie on the boundary of the figure  and inside the figure.)
and inside the figure.)
additional question:
b.) Find the area of the planar -neighborhood of a convex or non-convex polygon
-neighborhood of a convex or non-convex polygon 
c.) Find the volume of the -neighborhood of a convex polyhedron, e. g. of a cube or of a tetrahedron.
-neighborhood of a convex polyhedron, e. g. of a cube or of a tetrahedron.
Note by Darij: I guess that the '' -neighborhood'' of a figure is defined as the locus of all points whose distance to the figure is
-neighborhood'' of a figure is defined as the locus of all points whose distance to the figure is 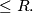
 be a convex polygon in a plane,
be a convex polygon in a plane,  its perimeter and
its perimeter and  its area. Let
its area. Let 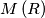 be the locus of all points in the space whose distance to
be the locus of all points in the space whose distance to  is
is 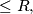 and
and 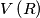 is the volume of the solid
is the volume of the solid 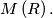
a.) Prove that
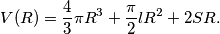
Hereby, we say that the distance of a point
 to a figure
to a figure  is
is 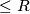 if there exists a point
if there exists a point  of the figure
of the figure  such that the distance
such that the distance  is
is 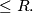 (This point
(This point  may lie on the boundary of the figure
may lie on the boundary of the figure  and inside the figure.)
and inside the figure.)additional question:
b.) Find the area of the planar
 -neighborhood of a convex or non-convex polygon
-neighborhood of a convex or non-convex polygon 
c.) Find the volume of the
 -neighborhood of a convex polyhedron, e. g. of a cube or of a tetrahedron.
-neighborhood of a convex polyhedron, e. g. of a cube or of a tetrahedron.Note by Darij: I guess that the ''
 -neighborhood'' of a figure is defined as the locus of all points whose distance to the figure is
-neighborhood'' of a figure is defined as the locus of all points whose distance to the figure is 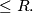
Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
