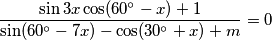
Find such that trigonometric where is a fixed real number.
%V0
Find $x$ such that trigonometric
$$\frac{\sin 3x \cos (60^\circ -x)+1}{\sin(60^\circ - 7x) - \cos(30^\circ + x) + m}=0$$
where $m$ is a fixed real number.
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
such that trigonometric 
is a fixed real number.