IMO Shortlist 1966 problem 12
Dodao/la:
arhiva2. travnja 2012. Find digits
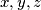
such that the equality

holds for at least two values of
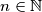
, and in that case find all

for which this equality is true.
%V0
Find digits $x, y, z$ such that the equality $$\sqrt{\underbrace{\overline{xx\cdots x}}_{n \text{ times}}-\underbrace{\overline{yy\cdots y}}_{n \text{ times}}}=\underbrace{\overline{zz\cdots z}}_{n \text{ times}}$$ holds for at least two values of $n \in \mathbb N$, and in that case find all $n$ for which this equality is true.
Izvor: Međunarodna matematička olimpijada, shortlist 1966