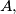
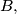
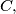
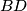
Given four points on a circle such that is a diameter and is not a diameter. Show that the line joining the point of intersection of the tangents to the circle at the points and with the point of intersection of the lines and is perpendicular to the line
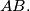
%V0
Given four points $A,$ $B,$ $C,$ $D$ on a circle such that $AB$ is a diameter and $CD$ is not a diameter. Show that the line joining the point of intersection of the tangents to the circle at the points $C$ and $D$ with the point of intersection of the lines $AC$ and $BD$ is perpendicular to the line $AB.$
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
on a circle such that 
is a diameter and 
is not a diameter. Show that the line joining the point of intersection of the tangents to the circle at the points 
and 
and 
is perpendicular to the line 