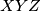
We are given a circle with center and radius and a square with center and side . Let be the hypotenuse of an isosceles right triangle . Describe the locus of points as varies along and varies along the boundary of
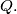
%V0
We are given a circle $K$ with center $S$ and radius $1$ and a square $Q$ with center $M$ and side $2$. Let $XY$ be the hypotenuse of an isosceles right triangle $XY Z$. Describe the locus of points $Z$ as $X$ varies along $K$ and $Y$ varies along the boundary of $Q.$
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
with center 
and radius 
and a square 
with center 
and side 
. Let 
be the hypotenuse of an isosceles right triangle 
. Describe the locus of points 
as 
varies along 
varies along the boundary of 