IMO Shortlist 1966 problem 17
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  and
and 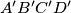 be two arbitrary parallelograms in the space, and let
be two arbitrary parallelograms in the space, and let 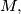
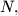
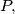
 be points dividing the segments
be points dividing the segments 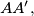
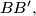
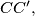
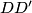 in equal ratios.
in equal ratios.
a.) Prove that the quadrilateral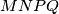 is a parallelogram.
is a parallelogram.
b.) What is the locus of the center of the parallelogram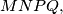 when the point
when the point  moves on the segment
moves on the segment 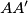 ?
?
(Consecutive vertices of the parallelograms are labelled in alphabetical order.
 and
and 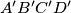 be two arbitrary parallelograms in the space, and let
be two arbitrary parallelograms in the space, and let 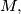
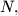
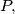
 be points dividing the segments
be points dividing the segments 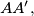
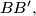
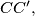
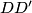 in equal ratios.
in equal ratios. a.) Prove that the quadrilateral
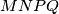 is a parallelogram.
is a parallelogram. b.) What is the locus of the center of the parallelogram
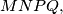 when the point
when the point  moves on the segment
moves on the segment 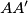 ?
? (Consecutive vertices of the parallelograms are labelled in alphabetical order.
Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
