IMO Shortlist 1966 problem 22
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  and
and 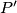 be two parallelograms with equal area, and let their sidelengths be
be two parallelograms with equal area, and let their sidelengths be 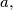
 and
and 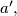
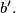 Assume that
Assume that 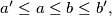 and moreover, it is possible to place the segment
and moreover, it is possible to place the segment 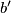 such that it completely lies in the interior of the parallelogram
such that it completely lies in the interior of the parallelogram 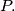
Show that the parallelogram can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram
can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram 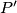 .
.
 and
and 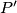 be two parallelograms with equal area, and let their sidelengths be
be two parallelograms with equal area, and let their sidelengths be 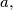
 and
and 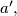
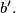 Assume that
Assume that 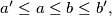 and moreover, it is possible to place the segment
and moreover, it is possible to place the segment 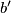 such that it completely lies in the interior of the parallelogram
such that it completely lies in the interior of the parallelogram 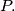
Show that the parallelogram
 can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram
can be partitioned into four polygons such that these four polygons can be composed again to form the parallelogram 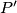 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
