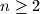
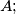
There are people at a meeting. Show that there exist two people at the meeting who have the same number of friends among the persons at the meeting. (It is assumed that if is a friend of then is a friend of moreover, nobody is his own friend.)
%V0
There are $n\geq 2$ people at a meeting. Show that there exist two people at the meeting who have the same number of friends among the persons at the meeting. (It is assumed that if $A$ is a friend of $B,$ then $B$ is a friend of $A;$ moreover, nobody is his own friend.)
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
people at a meeting. Show that there exist two people at the meeting who have the same number of friends among the persons at the meeting. (It is assumed that if 
is a friend of 
then 
is a friend of 
moreover, nobody is his own friend.)