IMO Shortlist 1966 problem 28
Dodao/la:
arhiva2. travnja 2012. In the plane, consider a circle with center

and radius
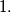
Let

be an arbitrary triangle having this circle as its incircle, and assume that
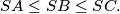
Find the locus of
a.) all vertices

of such triangles;
b.) all vertices

of such triangles;
c.) all vertices

of such triangles.
%V0
In the plane, consider a circle with center $S$ and radius $1.$ Let $ABC$ be an arbitrary triangle having this circle as its incircle, and assume that $SA\leq SB\leq SC.$ Find the locus of
a.) all vertices $A$ of such triangles;
b.) all vertices $B$ of such triangles;
c.) all vertices $C$ of such triangles.
Izvor: Međunarodna matematička olimpijada, shortlist 1966