IMO Shortlist 1966 problem 29
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 A given natural number  is being decomposed in a sum of some consecutive integers.
is being decomposed in a sum of some consecutive integers.
a.) Find all such decompositions for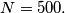
b.) How many such decompositions does the number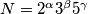 (where
(where 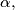
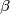 and
and  are natural numbers) have? Which of these decompositions contain natural summands only?
are natural numbers) have? Which of these decompositions contain natural summands only?
c.) Determine the number of such decompositions (= decompositions in a sum of consecutive integers; these integers are not necessarily natural) for an arbitrary natural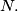
Note by Darij: The is not considered as a natural number.
is not considered as a natural number.
 is being decomposed in a sum of some consecutive integers.
is being decomposed in a sum of some consecutive integers. a.) Find all such decompositions for
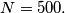
b.) How many such decompositions does the number
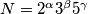 (where
(where 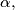
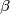 and
and  are natural numbers) have? Which of these decompositions contain natural summands only?
are natural numbers) have? Which of these decompositions contain natural summands only? c.) Determine the number of such decompositions (= decompositions in a sum of consecutive integers; these integers are not necessarily natural) for an arbitrary natural
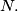
Note by Darij: The
 is not considered as a natural number.
is not considered as a natural number. Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
