IMO Shortlist 1966 problem 30
Dodao/la:
arhiva2. travnja 2012. Let

be a positive integer, prove that :
(a)
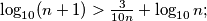
(b)
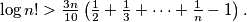
%V0
Let $n$ be a positive integer, prove that :
(a) $\log_{10}(n + 1) > \frac{3}{10n} +\log_{10}n ;$
(b) $\log n! > \frac{3n}{10}\left( \frac 12+\frac 13 +\cdots +\frac 1n -1\right).$
Izvor: Međunarodna matematička olimpijada, shortlist 1966