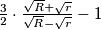
Two concentric circles have radii and respectively. Determine the greatest possible number of circles that are tangent to both these circles and mutually nonintersecting. Prove that this number lies between and
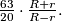
%V0
Two concentric circles have radii $R$ and $r$ respectively. Determine the greatest possible number of circles that are tangent to both these circles and mutually nonintersecting. Prove that this number lies between $\frac 32 \cdot \frac{\sqrt R +\sqrt r }{\sqrt R -\sqrt r } -1$ and $\frac{63}{20} \cdot \frac{R+r}{R-r}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
and 
respectively. Determine the greatest possible number of circles that are tangent to both these circles and mutually nonintersecting. Prove that this number lies between 
and 