IMO Shortlist 1966 problem 39
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Consider a circle with center  and radius
and radius 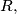 and let
and let  and
and  be two points in the plane of this circle.
be two points in the plane of this circle.
a.) Draw a chord of the circle such that
of the circle such that  is parallel to
is parallel to 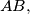 and the point of the intersection
and the point of the intersection  of the lines
of the lines  and
and  lies on the circle.
lies on the circle.
b.) Show that generally, one gets two possible points (
(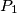 and
and 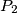 ) satisfying the condition of the above problem, and compute the distance between these two points, if the lengths
) satisfying the condition of the above problem, and compute the distance between these two points, if the lengths 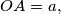
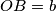 and
and 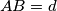 are given.
are given.
 and radius
and radius 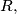 and let
and let  and
and  be two points in the plane of this circle.
be two points in the plane of this circle. a.) Draw a chord
 of the circle such that
of the circle such that  is parallel to
is parallel to 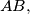 and the point of the intersection
and the point of the intersection  of the lines
of the lines  and
and  lies on the circle.
lies on the circle. b.) Show that generally, one gets two possible points
 (
(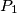 and
and 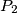 ) satisfying the condition of the above problem, and compute the distance between these two points, if the lengths
) satisfying the condition of the above problem, and compute the distance between these two points, if the lengths 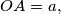
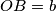 and
and 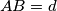 are given.
are given. Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
