IMO Shortlist 1966 problem 50
Dodao/la:
arhiva2. travnja 2012. Solve the equation
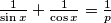
where

is a real parameter.
Discuss for which values of

the equation has at least one real solution and determine the number of solutions in
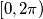
for a given
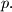
%V0
Solve the equation $\frac{1}{\sin x}+\frac{1}{\cos x}=\frac 1p$ where $p$ is a real parameter.
Discuss for which values of $p$ the equation has at least one real solution and determine the number of solutions in $[0, 2\pi)$ for a given $p.$
Izvor: Međunarodna matematička olimpijada, shortlist 1966