IMO Shortlist 1966 problem 52
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 A figure with area  is cut out of paper. We divide this figure into
is cut out of paper. We divide this figure into  parts and color them in
parts and color them in  different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in
different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in  parts again (in some different way). Show that we can color these new parts in the same
parts again (in some different way). Show that we can color these new parts in the same  colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is
colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is 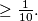
 is cut out of paper. We divide this figure into
is cut out of paper. We divide this figure into  parts and color them in
parts and color them in  different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in
different colors. Now, we turn around the piece of paper, divide the same figure on the other side of the paper in  parts again (in some different way). Show that we can color these new parts in the same
parts again (in some different way). Show that we can color these new parts in the same  colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is
colors again (hereby, different parts should have different colors) such that the sum of the areas of all parts of the figure colored with the same color on both sides is 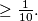
Izvor: Međunarodna matematička olimpijada, shortlist 1966
 Školjka
Školjka 
