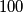
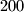
Is it possible to choose a set of (or ) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
%V0
Is it possible to choose a set of $100$ (or $200$) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.
Izvor: Međunarodna matematička olimpijada, shortlist 1966
Školjka 
(or 
) points on the boundary of a cube such that this set is fixed under each isometry of the cube into itself? Justify your answer.