IMO Shortlist 1967 problem 4
Dodao/la:
arhiva2. travnja 2012. Suppose medians
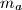
and
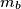
of a triangle are orthogonal. Prove that:
a.) Using medians of that triangle it is possible to construct a rectangular triangle.
b.) The following inequality:
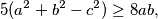
is valid, where
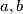
and

are side length of the given triangle.
%V0
Suppose medians $m_a$ and $m_b$ of a triangle are orthogonal. Prove that:
a.) Using medians of that triangle it is possible to construct a rectangular triangle.
b.) The following inequality: $$5(a^2+b^2-c^2) \geq 8ab,$$ is valid, where $a,b$ and $c$ are side length of the given triangle.
Izvor: Međunarodna matematička olimpijada, shortlist 1967