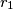
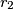
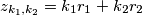
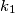
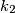
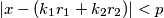
Prove the following statement: If and are real numbers whose quotient is irrational, then any real number can be approximated arbitrarily well by the numbers of the form integers, i.e. for every number and every positive real number two integers and can be found so that holds.
%V0
Prove the following statement: If $r_1$ and $r_2$ are real numbers whose quotient is irrational, then any real number $x$ can be approximated arbitrarily well by the numbers of the form $\ z_{k_1,k_2} = k_1r_1 + k_2r_2$ integers, i.e. for every number $x$ and every positive real number $p$ two integers $k_1$ and $k_2$ can be found so that $|x - (k_1r_1 + k_2r_2)| < p$ holds.
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
and 
are real numbers whose quotient is irrational, then any real number 
can be approximated arbitrarily well by the numbers of the form 
integers, i.e. for every number 
two integers 
and 
can be found so that 
holds.