IMO Shortlist 1967 problem 2
Dodao/la:
arhiva2. travnja 2012. If

is a positive rational number show that

can be uniquely expressed in the form
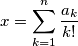
where
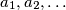
are integers,
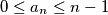
, for
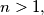
and the series terminates. Show that

can be expressed as the sum of reciprocals of different integers, each of which is greater than
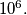
%V0
If $x$ is a positive rational number show that $x$ can be uniquely expressed in the form $\displaystyle x = \sum^n_{k=1} \frac{a_k}{k!}$ where $a_1, a_2, \ldots$ are integers, $0 \leq a_n \leq n - 1$, for $n > 1,$ and the series terminates. Show that $x$ can be expressed as the sum of reciprocals of different integers, each of which is greater than $10^6.$
Izvor: Međunarodna matematička olimpijada, shortlist 1967