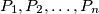
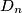
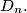
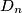
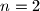
The points are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance between any two of these points has its largest possible value Calculate for to 7. and justify your answer.
%V0
The $n$ points $P_1,P_2, \ldots, P_n$ are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance $D_n$ between any two of these points has its largest possible value $D_n.$ Calculate $D_n$ for $n = 2$ to 7. and justify your answer.
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
points 
are placed inside or on the boundary of a disk of radius 1 in such a way that the minimum distance 
between any two of these points has its largest possible value 
Calculate 
to 7. and justify your answer.