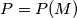
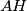
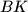
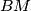
Let be a regular tetrahedron. To an arbitrary point on one edge, say , corresponds the point which is the intersection of two lines and , drawn from orthogonally to and from orthogonally to . What is the locus of when varies ?
%V0
Let $ABCD$ be a regular tetrahedron. To an arbitrary point $M$ on one edge, say $CD$, corresponds the point $P = P(M)$ which is the intersection of two lines $AH$ and $BK$, drawn from $A$ orthogonally to $BM$ and from $B$ orthogonally to $AM$. What is the locus of $P$ when $M$ varies ?
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
be a regular tetrahedron. To an arbitrary point 
on one edge, say 
, corresponds the point 
which is the intersection of two lines 
and 
, drawn from 
orthogonally to 
and from 
orthogonally to 
. What is the locus of 
when