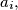
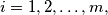
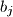
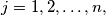
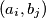
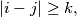
Given numbers: , determine the number of pairs for which where is a non-negative integer.
%V0
Given $m+n$ numbers: $a_i,$ $i = 1,2, \ldots, m,$ $b_j$, $j = 1,2, \ldots, n,$ determine the number of pairs $(a_i,b_j)$ for which $|i-j| \geq k,$ where $k$ is a non-negative integer.
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
numbers: 
, 
determine the number of pairs 
for which 
where 
is a non-negative integer.