IMO Shortlist 1967 problem 6
Dodao/la:
arhiva2. travnja 2012. Prove the identity
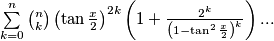
for any natural number

and any angle

%V0
Prove the identity
$\sum\limits_{k=0}^n\binom{n}{k}\left(\tan\frac{x}{2}\right)^{2k}\left(1+\frac{2^k}{\left(1-\tan^2\frac{x}{2}\right)^k}\right)...$
for any natural number $n$ and any angle $x.$
Izvor: Međunarodna matematička olimpijada, shortlist 1967