IMO Shortlist 1967 problem 3
Dodao/la:
arhiva2. travnja 2012. Prove that for arbitrary positive numbers the following inequality holds
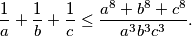
%V0
Prove that for arbitrary positive numbers the following inequality holds
$$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \leq \frac{a^8 + b^8 + c^8}{a^3b^3c^3}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
