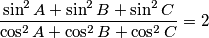
Show that a triangle whose angles , , satisfy the equality is a rectangular triangle.
%V0
Show that a triangle whose angles $A$, $B$, $C$ satisfy the equality
$$\frac{\sin^2 A + \sin^2 B + \sin^2 C}{\cos^2 A + \cos^2 B + \cos^2 C} = 2$$
is a rectangular triangle.
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
, 
, 
satisfy the equality 