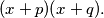
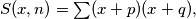
Suppose that and are two different positive integers and is a real number. Form the product Find the sum where and take values from 1 to Does there exist integer values of for which
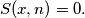
%V0
Suppose that $p$ and $q$ are two different positive integers and $x$ is a real number. Form the product $(x+p)(x+q).$ Find the sum $S(x,n) = \sum (x+p)(x+q),$ where $p$ and $q$ take values from 1 to $n.$ Does there exist integer values of $x$ for which $S(x,n) = 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
and 
are two different positive integers and 
is a real number. Form the product 
Find the sum 
where 
Does there exist integer values of 