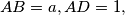
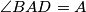
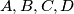
The parallelogram has , and the triangle has all angles acute. Prove that circles radius and center cover the parallelogram if and only
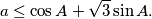
%V0
The parallelogram $ABCD$ has $AB=a,AD=1,$ $\angle BAD=A$, and the triangle $ABD$ has all angles acute. Prove that circles radius $1$ and center $A,B,C,D$ cover the parallelogram if and only
$$a\le\cos A+\sqrt3\sin A.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
has 
, and the triangle 
has all angles acute. Prove that circles radius 
and center 
cover the parallelogram if and only 