IMO Shortlist 1967 problem 1
Dodao/la:
arhiva2. travnja 2012. Let
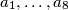
be reals, not all equal to zero. Let
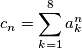
for
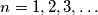
. Given that among the numbers of the sequence
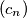
, there are infinitely many equal to zero, determine all the values of

for which
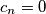
.
%V0
Let $a_1,\ldots,a_8$ be reals, not all equal to zero. Let $$\displaystyle c_n = \sum^8_{k=1} a^n_k$$ for $n=1,2,3,\ldots$. Given that among the numbers of the sequence $(c_n)$, there are infinitely many equal to zero, determine all the values of $n$ for which $c_n = 0$.
Izvor: Međunarodna matematička olimpijada, shortlist 1967