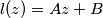
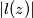
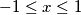
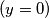
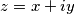
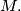
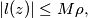
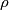
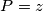
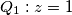
A linear binomial with complex coefficients and is given. It is known that the maximal value of on the segment of the real line in the complex plane is equal to Prove that for every where is the sum of distances from the point to the points and
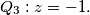
%V0
A linear binomial $l(z) = Az + B$ with complex coefficients $A$ and $B$ is given. It is known that the maximal value of $|l(z)|$ on the segment $-1 \leq x \leq 1$ $(y = 0)$ of the real line in the complex plane $z = x + iy$ is equal to $M.$ Prove that for every $z$
$$|l(z)| \leq M \rho,$$
where $\rho$ is the sum of distances from the point $P=z$ to the points $Q_1: z = 1$ and $Q_3: z = -1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
with complex coefficients 
and 
is given. It is known that the maximal value of 
on the segment 
of the real line in the complex plane 
is equal to 
Prove that for every 
is the sum of distances from the point 
to the points 
and 