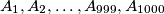
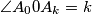
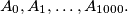
On the circle with center 0 and radius 1 the point is fixed and points are distributed in such a way that the angle (in radians). Cut the circle at points How many arcs with different lengths are obtained. ?
%V0
On the circle with center 0 and radius 1 the point $A_0$ is fixed and points $A_1, A_2, \ldots, A_{999}, A_{1000}$ are distributed in such a way that the angle $\angle A_00A_k = k$ (in radians). Cut the circle at points $A_0, A_1, \ldots, A_{1000}.$ How many arcs with different lengths are obtained. ?
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
is fixed and points 
are distributed in such a way that the angle 
(in radians). Cut the circle at points 
How many arcs with different lengths are obtained. ?