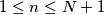
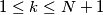
Let and be positive integers such that , . Show that:
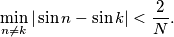
%V0
Let $n$ and $k$ be positive integers such that $1 \leq n \leq N+1$, $1 \leq k \leq N+1$. Show that: $$\min_{n \neq k} |\sin n - \sin k| < \frac{2}{N}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
and 
be positive integers such that 
, 
. Show that: 