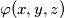
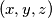
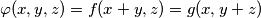
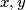
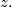
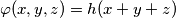
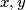
The function defined for all triples of real numbers, is such that there are two functions and defined for all pairs of real numbers, such that for all real numbers and Show that there is a function of one real variable, such that for all real numbers and
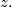
%V0
The function $\varphi(x,y,z)$ defined for all triples $(x,y,z)$ of real numbers, is such that there are two functions $f$ and $g$ defined for all pairs of real numbers, such that
$$\varphi(x,y,z) = f(x+y,z) = g(x,y+z)$$
for all real numbers $x,y$ and $z.$ Show that there is a function $h$ of one real variable, such that
$$\varphi(x,y,z) = h(x+y+z)$$
for all real numbers $x,y$ and $z.$
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
defined for all triples 
of real numbers, is such that there are two functions 
and 
defined for all pairs of real numbers, such that 
and 
Show that there is a function 
of one real variable, such that 