IMO Shortlist 1968 problem 5
Dodao/la:
arhiva2. travnja 2012. Let
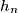
be the apothem (distance from the center to one of the sides) of a regular

-gon (

) inscribed in a circle of radius

. Prove the inequality
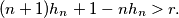
Also prove that if

on the right side is replaced with a greater number, the inequality will not remain true for all
%V0
Let $h_n$ be the apothem (distance from the center to one of the sides) of a regular $n$-gon ($n \geq 3$) inscribed in a circle of radius $r$. Prove the inequality
$$(n + 1)h_n+1 - nh_n > r.$$
Also prove that if $r$ on the right side is replaced with a greater number, the inequality will not remain true for all $n \geq 3.$
Izvor: Međunarodna matematička olimpijada, shortlist 1968