IMO Shortlist 1968 problem 9
Dodao/la:
arhiva2. travnja 2012. Let

be an arbitrary triangle and

a point inside it. Let
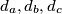
be the distances from

to sides
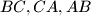
;
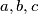
the lengths of the sides respectively, and

the area of the triangle

. Prove the inequality
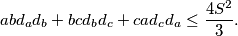
Prove that the left-hand side attains its maximum when

is the centroid of the triangle.
%V0
Let $ABC$ be an arbitrary triangle and $M$ a point inside it. Let $d_a, d_b, d_c$ be the distances from $M$ to sides $BC,CA,AB$; $a, b, c$ the lengths of the sides respectively, and $S$ the area of the triangle $ABC$. Prove the inequality
$$abd_ad_b + bcd_bd_c + cad_cd_a \leq \frac{4S^2}{3}.$$
Prove that the left-hand side attains its maximum when $M$ is the centroid of the triangle.
Izvor: Međunarodna matematička olimpijada, shortlist 1968