IMO Shortlist 1968 problem 10
Dodao/la:
arhiva2. travnja 2012. Consider two segments of length
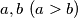
and a segment of length
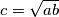
.
(a) For what values of
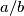
can these segments be sides of a triangle ?
(b) For what values of
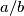
is this triangle right-angled, obtuse-angled, or acute-angled ?
%V0
Consider two segments of length $a, b \ (a > b)$ and a segment of length $c = \sqrt{ab}$.
(a) For what values of $a/b$ can these segments be sides of a triangle ?
(b) For what values of $a/b$ is this triangle right-angled, obtuse-angled, or acute-angled ?
Izvor: Međunarodna matematička olimpijada, shortlist 1968