IMO Shortlist 1968 problem 11
Dodao/la:
arhiva2. travnja 2012. Find all solutions
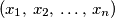
of the equation
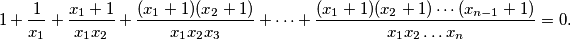
%V0
Find all solutions $(x_1,\,x_2,\,\ldots ,\,x_n)$ of the equation
$$1 + \frac{1}{x_1} + \frac{x_1+1}{x_1x_2} + \frac{(x_1+1)(x_2+1)}{x_1x_2x_3} + \cdots + \frac{(x_1+1)(x_2+1) \cdots (x_{n-1}+1)}{x_1x_2 \ldots x_n} = 0\text{.}$$
Izvor: Međunarodna matematička olimpijada, shortlist 1968