If and are arbitrary positive real numbers and an integer, prove that
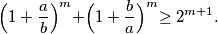
%V0
If $a$ and $b$ are arbitrary positive real numbers and $m$ an integer, prove that
$$\Bigr( 1+\frac ab \Bigl)^m +\Bigr( 1+\frac ba \Bigl)^m \geq 2^{m+1}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1968
Školjka 
and 
are arbitrary positive real numbers and 
an integer, prove that