IMO Shortlist 1968 problem 17
Dodao/la:
arhiva2. travnja 2012. Given a point

and lengths
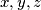
, prove that there exists an equilateral triangle

for which
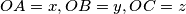
, if and only if
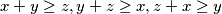
(the points
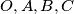
are coplanar).
%V0
Given a point $O$ and lengths $x, y, z$, prove that there exists an equilateral triangle $ABC$ for which $OA = x, OB = y, OC = z$, if and only if $x+y \geq z, y+z \geq x, z+x \geq y$ (the points $O,A,B,C$ are coplanar).
Izvor: Međunarodna matematička olimpijada, shortlist 1968