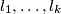
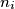
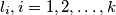
Given parallel lines and points on the line , find the maximum possible number of triangles with vertices at these points.
%V0
Given $k$ parallel lines $l_1, \ldots, l_k$ and $n_i$ points on the line $l_i, i = 1, 2, \ldots, k$, find the maximum possible number of triangles with vertices at these points.
Izvor: Međunarodna matematička olimpijada, shortlist 1968
Školjka 
parallel lines 
and 
points on the line 
, find the maximum possible number of triangles with vertices at these points.