IMO Shortlist 1968 problem 25
Dodao/la:
arhiva2. travnja 2012. Let

be a real-valued function defined for all real numbers, such that for some
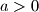
we have
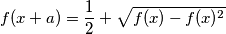
for all

.
Prove that

is periodic, and give an example of such a non-constant

for
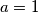
.
%V0
Let $f$ be a real-valued function defined for all real numbers, such that for some $a>0$ we have $$f(x+a)={1\over2}+\sqrt{f(x)-f(x)^2}$$ for all $x$.
Prove that $f$ is periodic, and give an example of such a non-constant $f$ for $a=1$.
Izvor: Međunarodna matematička olimpijada, shortlist 1968