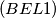
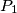
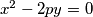
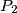
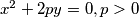
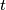
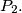
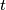
A parabola with equation and parabola with equation , are given. A line is tangent to Find the locus of pole of the line with respect to
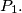
%V0
$(BEL 1)$ A parabola $P_1$ with equation $x^2 - 2py = 0$ and parabola $P_2$ with equation $x^2 + 2py = 0, p > 0$, are given. A line $t$ is tangent to $P_2.$ Find the locus of pole $M$ of the line $t$ with respect to $P_1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
A parabola 
with equation 
and parabola 
with equation 
, are given. A line 
is tangent to 
Find the locus of pole 
of the line 