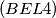
Let be a point on a nondegenerate conic. A right angle with vertex intersects the conic at points and . Prove that the line passes through a fixed point located on the normal to the conic through the point
%V0
$(BEL 4)$ Let $O$ be a point on a nondegenerate conic. A right angle with vertex $O$ intersects the conic at points $A$ and $B$. Prove that the line $AB$ passes through a fixed point located on the normal to the conic through the point $O.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
be a point on a nondegenerate conic. A right angle with vertex 
and 
. Prove that the line 
passes through a fixed point located on the normal to the conic through the point 