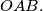
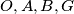
Let be the centroid of the triangle Prove that all conics passing through the points are hyperbolas. Find the locus of the centers of these hyperbolas.
%V0
$(BEL 5)$ Let $G$ be the centroid of the triangle $OAB.$
$(a)$ Prove that all conics passing through the points $O,A,B,G$ are hyperbolas.
$(b)$ Find the locus of the centers of these hyperbolas.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Let 
be the centroid of the triangle 
Prove that all conics passing through the points 
are hyperbolas.
Find the locus of the centers of these hyperbolas.