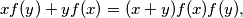
Find all functions defined for all that satisfy the condition for all and Prove that exactly two of them are continuous.
%V0
$(BUL 2)$ Find all functions $f$ defined for all $x$ that satisfy the condition $xf(y) + yf(x) = (x + y)f(x)f(y),$ for all $x$ and $y.$ Prove that exactly two of them are continuous.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
Find all functions 
defined for all 
that satisfy the condition 
for all 
Prove that exactly two of them are continuous.