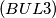
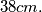
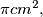
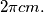
One hundred convex polygons are placed on a square with edge of length The area of each of the polygons is smaller than and the perimeter of each of the polygons is smaller than Prove that there exists a disk with radius in the square that does not intersect any of the polygons.
%V0
$(BUL 3)$ One hundred convex polygons are placed on a square with edge of length $38 cm.$ The area of each of the polygons is smaller than $\pi cm^2,$ and the perimeter of each of the polygons is smaller than $2\pi cm.$ Prove that there exists a disk with radius $1$ in the square that does not intersect any of the polygons.
Izvor: Međunarodna matematička olimpijada, shortlist 1969
Školjka 
One hundred convex polygons are placed on a square with edge of length 
The area of each of the polygons is smaller than 
and the perimeter of each of the polygons is smaller than 
Prove that there exists a disk with radius 
in the square that does not intersect any of the polygons.